where d1 ≤ d2 ≤ ... ≤ d1. Suppose that dj ≥ j, for j=1, 2, ..., n-1-dn. Show that G is connected.
(d1, d2, ...,dn) iff Σ di = 2(n-1), where each di > 0. Hint: think of a leaf.
|
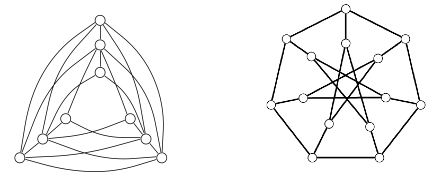
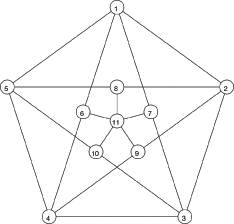
1. Determine whether the following graphs are hamiltonian. Explain.
|
|
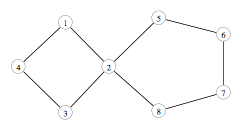
2. Determine whether the following graphs are isomorphic. Explain.
|
| 4. Find a 2-cell embedding of K4,4 on the torus, if possible. |
| 5. Find a 2-cell embedding of K4,5 on the torus, if possible. |
| 6. Find a 2-cell embedding of K4,4 on the projective plane, if possible. |
| 7. How many perfect matchings does the graph of the cube have ? How many 1-factorizations ? |
| 8. Let A be the adjacency matrix of a graph G. What does entry [i,j] of A2 represent ? What about A3 ? |
| 9. Show that a tournament on n vertices always contains a directed Hamiltonian path. |
| 10. Let G be a graph on n vertices, and let T be any tree on n vertices. Show that the problem of determining whether G has a spanning tree isomorphic to T is NP-complete. You can assume that the HamCycle problem is NP-complete. |
|
11. Let d1, d2, ...,dn be the degree sequence of a graph G, where d1 ≤ d2 ≤ ... ≤ d1. Suppose that dj ≥ j, for j=1, 2, ..., n-1-dn. Show that G is connected. |
|
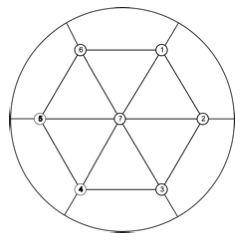
12. Find a TK5 in the following projective graph.
 |
| 13. Prove that in a connected graph, any two longest paths have at least one vertex in common. |
| 14. Describe an algorithm for finding an edge uv in a network such that the value of a max flow can be increased if cap(uv) is increased, if there is such an edge. |
15. Find the chromatic polynomial of the graph shown.
 |
|
16. Show that for any n > 1, there is a tree with degree sequence (d1, d2, ...,dn) iff Σ di = 2(n-1), where each di > 0. Hint: think of a leaf. |
17. Find an embedding of the following graph on the projective plane and torus, if possible.
 |
| 18. A saturated hydrocarbon is a molecule CmHn in which every carbon atom has valence four and every hydrogen atom has valence one, and no sequence of atoms forms a cycle. Show that for every positive integer m, CmHn can exist only if n = 2m + 2. |
| 19. Let G be a graph with n vertices. Replace each edge of G with m multiple edges to get a graph Gm. Prove that τ(Gm) = mn-1 τ(G). |
|
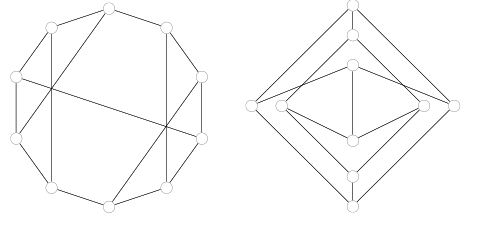
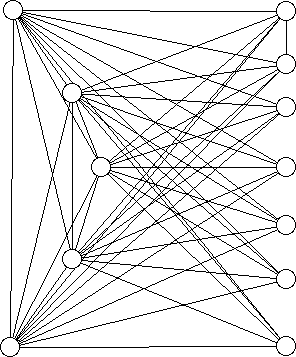
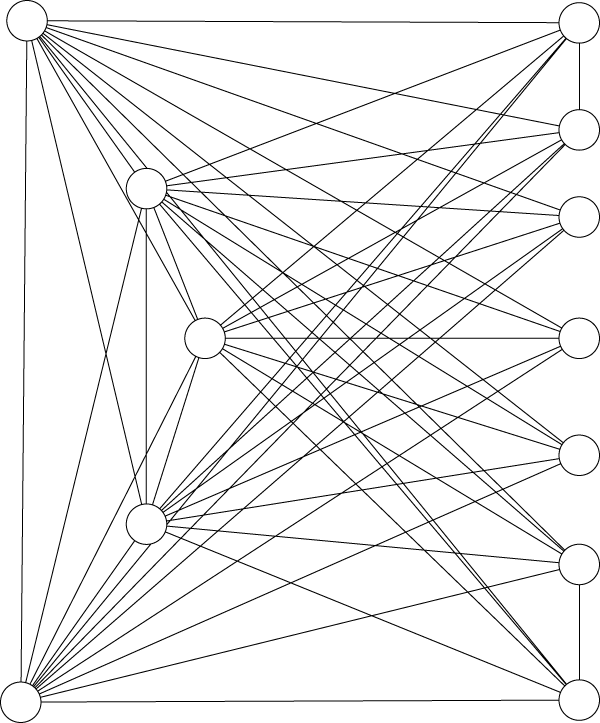
20. Determine whether or not the graphs shown are hamiltonian. Explain.
|
| 21. If possible, draw an eulerian graph with n even and e odd; otherwise explain why there is no such graph. |
|
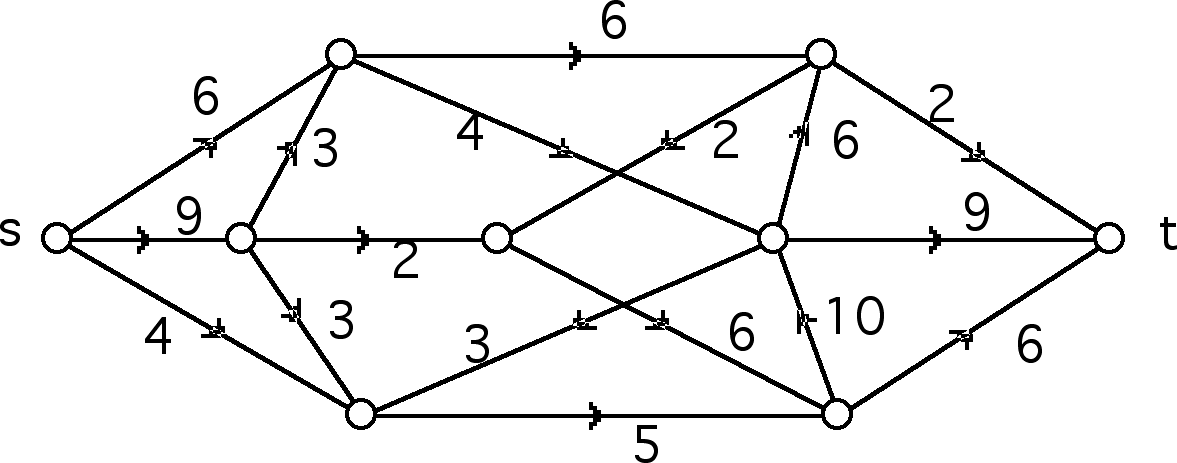
22. Find a max flow f in the network shown. Prove your flow is maximum by illustrating a minimum edge-cut K such that val(f) = cap(K).
|