For additional information, see the research project descriptions for
Steph
Durocher
and Jason
Morrison.
Local Routing in Wireless Networks
Overview
A local routing algorithm makes a sequence of distributed forwarding decisions,
each of which is made using only local information.
Specifically, in addition to knowing the node for which a message is destined,
an intermediate node might also know:
- the node from which the message originated,
- which of its neighbours last forwarded the message, and
- the subgraph corresponding to all network nodes within k hops of
itself, for some value of k.
We examine theoretical bounds on the locality of routing.
Our objective is to determine which of these parameters are necessary and/or
sufficient to permit local routing as k varies on a network modelled by a
connected undirected graph.
Our results include:
- showing that no k-local routing algorithm succeeds on
unit ball graphs for any fixed k
when nodes are location-aware,
- establishing tight bounds on k for the feasibility of
deterministic k-local routing under various combinations of these
parameters, and
- establishing tight bounds on the dilation
(the worst-case ratio of actual route length to shortest path length)
for k-local routing algorithms.
Project Members
Stephane Durocher,
Debajyoti Mondal,
Maxime Peabody,
Matthew Skala,
Mohammad Abdul Wahid
Collaborators
David Kirkpatrick,
Lata Narayanan,
Prosenjit Bose,
Paz Carmi,
Jean-Lou de Carufel,
Alireza Haghnegahdar,
Majid Khabbazian,
Fabian Kuhn,
Perouz Taslakian
Publications
SOFSEM 2015,
TON 2014,
SWAT 2014,
SIROCCO 2012,
Distributed Computing 2012,
Wireless Networks 2010,
PODC 2009,
ICDCN 2008
Facility Location
in Wireless Networks
Overview
When wireless nodes are represented by points in Euclidean space,
networks edges are defined by a geometric proximity graph,
and the distance between two nodes is measured by the number of network hops
on a shortest path connecting them, the resulting facility location problems
are set neither solely in Euclidean space nor on a graph.
Although similar to problems of facility location in both settings,
existing solutions do not necessarily apply to this new combination of
graph-theoretic and geometric constraints.
Unit disc graphs are proximity graphs that are frequently
used to model wireless networks.
We consider the k-centre problem on unit disc graphs: given a set of
points P in the plane, find a set F of k points in the plane that minimizes
the maximum graph distance from any vertex in P to the nearest vertex
in F in the unit disc graph induced by P ∪ F.
We describe exact and approximate polynomial-time solutions to this problem
for any fixed k and
show that the problem is NP-hard when k is an arbitrary input parameter.
Project Members
Stephane Durocher,
Saeed Mehrabi
Collaborators
Krishnam Raju Jampani,
Anna Lubiw,
Lata Narayanan,
Publications
CGTA 2011,
DIAML-POMC 2008
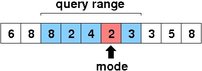
Array Range Query
Overview
Given a list A[1:n] of n items, we consider the problem of constructing
a (typically linear-sapce) data structure
that efficiently answers subsequent range frequency queries on A.
Each query consists of an input pair of indices (i, j)
for which a particular statistic of A[i:j] must be returned
(e.g., a mode, minimum, least-frequent element, minority, or majority).
Project Members
Stephane Durocher,
Jason Morrison,
Matthew Skala
Collaborators
Timothy Chan,
Meng He,
Kasper Green Larsen,
Ian Munro,
Patrick Nicholson,
Rahul Shah,
Sharma Thankachan,
Bryan Wilkinson
Publications
Algorithmica 2014,
Algorithmica 2014,
TOCS 2014,
CCCG 2014,
SPIRE 2013,
MFCS 2013,
Munro Festschrift 2013,
ToCS 2013,
InfoComp 2013,
SWAT 2012,
STACS 2012,
ICALP 2011

Graph Drawing
Overview
Debajyoti Mondal
is a Ph.D. student in the Computational Geometry Laboratory
working on problems in graph drawing, including results on:
- minimum-segment drawings of planar graphs,
- plane 3-trees,
- thickness and colourability,
- pairwise compatibility graphs, and
- point-set embeddings.
Project Members
Stephane Durocher,
Saeed Mehrabi,
Debajyoti Mondal
Collaborators
Stefan Felsner,
Ellen Gethner,
Rahnuma Islam Nishat,
Md. Saidur Rahman,
Sue Whitesides
Publications
SIDMA 2015,
GD 2014,
GD 2014,
CCCG 2014,
LATIN 2014,
GD 2013,
JGAA 2013,
WADS 2013,
WG 2013,
WALCOM 2013,
WALCOM 2012,
COCOA 2012,
GD 2011,
CCCG 2011
Geometric Optimization
Overview
Saeed Mehrabi
is a Ph.D. in the Computational Geometry Laboratory
working on algorithms for exact
and approximate solutions to problems
in geometric optimization, including results on:
- sliding cameras
(art galleries with line segment guards), and
- partitions with minimum stabbing number.
Project Members
Stephane Durocher,
Omrit Filtser,
Bob Fraser,
Ali Mehrabi,
Saeed Mehrabi
Publications
COCOA 2014,
IWOCA 2014,
LATIN 2014,
MFCS 2013,
COCOON 2012